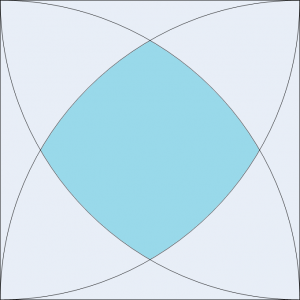
小学校の頃、自分は塾には行っていなかったのだが、
デニム地にNと書かれたカバンをしょって塾に行っていたある友人から、
塾で仕入れた算数の問題を出題されて解く、という遊び(?)をよくやっていた。
その中で非常に印象に残っている問題があったので、紹介してみたい。
問題(Q1とする)
正方形の中に正方形の一辺を半径として描かれた4つの1/4扇型、
そのかこまれた中央の面積を求めるという問題である。
一辺の長さは、当時いくつで与えられたかは覚えていないが、
1cmとか10cmとかだったと思う。
今解くに当たって、計算は1がやりやすいが、一般解を求めるなら
aとかにしておいた方が良さそうなので、仮にaとする。
果たして解けるだろうか。
この問題の面白いところは、小学校でその段階を踏んでいるところにあると思う。
最初に円の面積の求め方を習って、その後扇型の面積を習う。
その後、こういう問題が出てくる。(Q2とする)
さらに、その応用でこういう問題が出てくる。(Q3とする)
Q1の問題は、いかにもQ2,Q3の延長で解けそうなところにその面白みがある。
しかし結論から言うと、小学校の学習範囲でQ1を解くことは出来ない。
自分もやはり、これをその時解くことは出来なかった。
その友人も答えは分からず、悲しいことに周りにこれの解き方を
教えてくれる(考えてくれる)大人も居なかった。(先生に聞いても分からなかった)
結局自分でこれが解けたのは中学3年生になってからである。
いや、「答え」は結局のところないので、自分の答えが合っているかどうか、
確認する術はない。ただ、解けている気がするというだけだ。
ここで言いたいのは、ずっとこの問題のことを覚え続けていた（結果解けた）ことが、
自分の中の「勉強することの意味」を支えていると思っていることだ。
私はこの問題が解けなかった（当時おそらく5年生か6年生だった)ときからずっと、
ふとした時にこの問題を思い出しては、解けないかと頑張ってみたものだった。
その結果として中学3年生の時に自分の力でこれを解くことが出来た、
その時は「勉強してきて良かった」、そんな言葉では言い表わせられないほどの喜びを
感じたことを覚えている。
また、算出される答えがかなり美しいということも、解けた時のすっきり感と喜びをことさら大きくしている。
今でも、何か分からなかったことをずっと考え続けていたら、
ある時急にひらめいて腑に落ちていく、ということがしばしばあり、
「時間をかけて考えれば絶対に答えにたどり着くはず」という
漠然とした自信につながっている。
それは「考え続けることの意味」を実体験として持っているということが大きい。
今やインターネットで分からないことはないと言えるほど「答え」が溢れていると思う。
「簡単に答えにたどり着いてしまう世界」って
実はこういう体験機会を極端に減らしてしまっているのではないかなと思う。
そんな願いも込めて、この問題の答え（というか自分の辿り着いた解法）は
書かないことにしたいが、それもあんまりなので解法に繋がる補助線を引いた画像だけ
ここに置いておこうと思う。
この問題が誰かの「考えること」のきっかけになってくれたら嬉しい。
あと他のもっとスマートな解法を思いついたらそっと教えてほしい…。
—-追記—–
この記事を書いた後、何気なく違うやり方を考えてみたら、
このやり方でも解けることに気付いた。
しかもこのやり方だと計算がすごく楽だ。
なんだろう。何でもやってみるもんだな。
